How is resolution computed

Index

• Normal distribution

• Resolution

• Relative scaling

• Error bars

import numpy as np
import matplotlib.pyplot as plt
from ctaplot.ana import resolution, relative_scaling

Normal distribution

For a nomal distribution, corresponds to the 68 percentile of the distribution

See the 68–95–99.7 rule

loc = 10
scale = 3

X = np.random.normal(size=1000000, scale=scale, loc=loc)
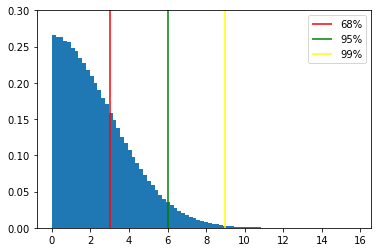
plt.hist(np.abs(X - loc), bins=80, density=True)

sig_68 = np.percentile(np.abs(X - loc), 68.27)
sig_95 = np.percentile(np.abs(X - loc), 95.45)
sig_99 = np.percentile(np.abs(X - loc), 99.73)

plt.vlines(sig_68, 0, 0.3, label='68%', color='red')
plt.vlines(sig_95, 0, 0.3, label='95%', color='green')
plt.vlines(sig_99, 0, 0.3, label='99%', color='yellow')
plt.ylim(0,0.3)
plt.legend()


print("68th percentile = {:.4f}".format(sig_68))
print("95th percentile = {:.4f}".format(sig_95))
print("99th percentile = {:.4f}".format(sig_99))

assert np.isclose(sig_68, scale, rtol=1e-2)
assert np.isclose(sig_95, 2 * scale, rtol=1e-2)
assert np.isclose(sig_99, 3 * scale, rtol=1e-2)

68th percentile = 2.9999
95th percentile = 6.0005
99th percentile = 8.9907

Resolution

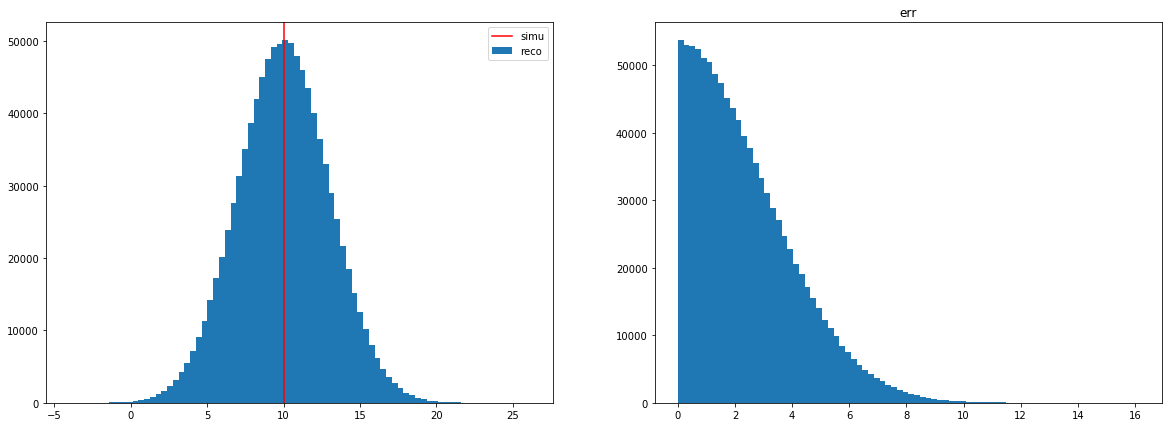
The resolution is defined as the 68th percentile of the relative error err = (reco - simu)/scaling.

(see the relative scaling section for more info on it).

Hence, if the relative error follows a normal distribution, the resolution is equal to the sigma of the distribution

simu = loc * np.ones(X.shape[0])
reco = np.random.normal(loc=loc, scale=scale, size=X.shape[0])

err = np.abs(simu - reco)

fig, axes = plt.subplots(1, 2, figsize=(20,7))
axes[0].hist(reco, bins=80, label='reco')
axes[0].axvline(loc, 0, 1, color='red', label='simu')
axes[0].legend()
axes[1].hist(err, bins=80)
axes[1].set_title('err')

Text(0.5, 1.0, 'err')

Let’s define reco in order to have a relative error equals to err.

Its resolution is equals to the sigma of the distribution

res = resolution(simu, reco, relative_scaling_method=None)
print(res)
assert np.isclose(res[0], scale, rtol=1e-2)

[3.0029721  2.99821785 3.00797764]

---

Relative scaling

The resolution can be measured on the absolute error or on the relative one.

There is no absolute definition of the relative scaling and several are proposed in ctaplot.

The choice can be passed through the relative_scaling_method:

Methods:

- s0 : no scaling (scaling = 1)

- s1 : $ scaling = |simu| $

- s2 : $ scaling = |reco| $

- s3 : $ scaling = (|simu\| + \|reco|)/2 $

- s4 : $ scaling = max(|reco|, |simu|) $

The default one for the resolution is s1.

Note that methods involving reco are more subject to deviation from the expected result:

for method in ['s1', 's2', 's3', 's4']:
    res = resolution(simu, reco, relative_scaling_method=method)
    print("Method {} gives a resolution = {:.3f} to be compared with the expected value = {}".format(method, res[0], scale/loc))

Method s1 gives a resolution = 0.300 to be compared with the expected value = 0.3
Method s2 gives a resolution = 0.288 to be compared with the expected value = 0.3
Method s3 gives a resolution = 0.297 to be compared with the expected value = 0.3
Method s4 gives a resolution = 0.259 to be compared with the expected value = 0.3

NB:

- the angular resolution uses no scaling

- the energy resolution uses scaling s1

- the impact resolution uses no scaling by default

---

Error bars

Errors bars in resolution plots are given by the confidence interval (by default at 95%, equivalent to 2 sigmas for a normal distribution).

This means that we can be confident at 95% that the resolution values are within the range given by the error bars.

The implementation for percentile confidence interval follows: - http://people.stat.sfu.ca/~cschwarz/Stat-650/Notes/PDF/ChapterPercentiles.pdf

Example with a normal distribution:

nbins, bins, patches = plt.hist(X, bins=100, density=True)
ymax = 1.1 * nbins.max()
plt.ylim(0, ymax)
plt.vlines(np.percentile(X, 68.27), 0, ymax, color='red')
plt.show()
print("The true 68th percentile of this distribution is: {:.4f}".format(np.percentile(X, 68.27)))

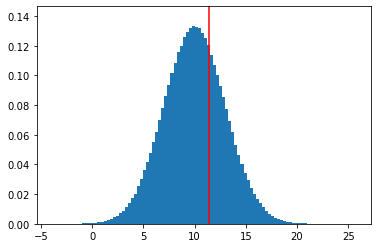
The true 68th percentile of this distribution is: 11.4226

We can consider this as our underlying (infinite) distribution.

If we take a random sample in this ditribution, the measurement of a percentile will come with a measurement error. We can assess this error by taking multiple random samples and taking the distribution of measured percentile values.

n = 1000
p = 0.6827
all_68 = []
for i in range(int(len(X)/n)):
    all_68.append(np.percentile(X[i*n:(i+1)*n], p*100))

all_68 = np.array(all_68)
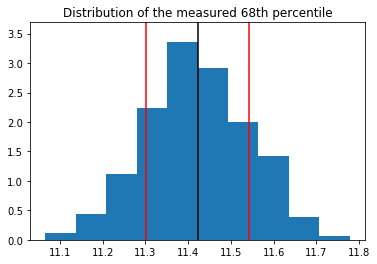
nbins, bins, patches = plt.hist(all_68, density=True);
ymax = 1.1 * nbins.max()
plt.vlines(all_68.mean(), 0, ymax)
plt.vlines(all_68.mean() + all_68.std(), 0, ymax, color='red')
plt.vlines(all_68.mean() - all_68.std(), 0, ymax, color='red')
plt.ylim(0, ymax)
plt.title("Distribution of the measured 68th percentile")

print("Standard deviation = {:.5f}".format(all_68.std()))

Standard deviation = 0.11973

To evaluate directly the confidence interval from a sub-sample of the distribution, one can use the following formulae:

$ R_{low} = np − z \sqrt{n * p * (1 − p)} $

$ R_{up} = np + z \sqrt{n * p * (1 − p)} $

with the percentile and the confidence level desired.

And the confidence interval given by: (

The confidence level is given by the cumulative distribution function (scipy.stats.norm.ppf).

Some useful values:

• z = 0.47 for a confidence level of 68%

• z = 1.645 for a confidence level of 95%

• z = 2.33 for a confidence level of 99%

# confidence level:
z = 2.33

# sub-sample:
x = X[:n]

rl = int(n * p - z * np.sqrt(n * p * (1-p)))
ru = int(n * p + z * np.sqrt(n * p * (1-p)))
print("Measured percentile: {:.4f}".format(np.percentile(x, p*100)))
print("Confidence interval: ({:.4f}, {:.4f})".format(np.sort(x)[rl], np.sort(x)[ru]))
print("To be compared with: ({:.4f}, {:.4f})".format(all_68.mean()-all_68.std()*3, all_68.mean()+all_68.std()*3))
print("which is the corresponding confidence interval given by the normal distribution of the measured percentiles")

Measured percentile: 11.5283
Confidence interval: (11.2443, 11.9176)
To be compared with: (11.0628, 11.7812)
which is the corresponding confidence interval given by the normal distribution of the measured percentiles

In ctaplot, this is computed by the function percentile_confidence interval:

from ctaplot.ana import percentile_confidence_interval

p = 68.27
confidence_level = 0.99
pci = percentile_confidence_interval(x, percentile=p, confidence_level=0.99)
print("68th percentile: {:.3f}".format(np.percentile(x, p)))
print("Interval with a confidence level of {}%: ({:.3f}, {:.3f})".format(confidence_level*100, pci[0], pci[1]))


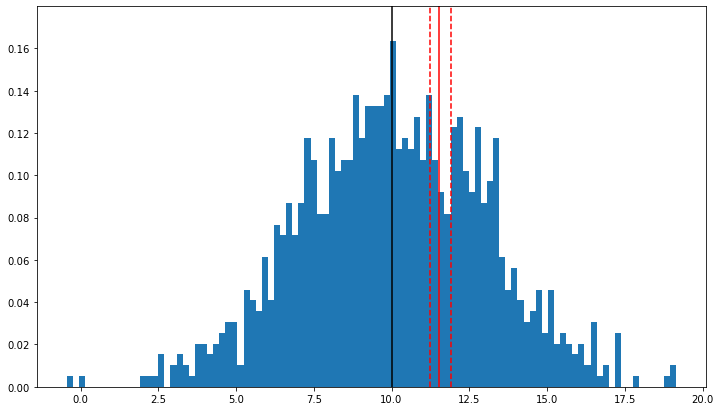
plt.figure(figsize=(12,7))
nbins, bins, patches = plt.hist(x, bins=100, density=True);
ymax = 1.1 * nbins.max()

plt.vlines(np.percentile(x, 50), 0, ymax, color='black')
plt.vlines(np.percentile(x, p), 0, ymax, color='red')
plt.vlines(pci[0], 0, ymax, linestyles='--', color='red')
plt.vlines(pci[1], 0, ymax, linestyles='--', color='red',)
plt.ylim(0, ymax);

68th percentile: 11.528
Interval with a confidence level of 99.0%: (11.244, 11.918)

---

Note: The same method could be applied around the median.

In this case, the confidence interval is also given by for a normal distribution.

pci = percentile_confidence_interval(X, percentile=50, confidence_level=0.99)
print("Median: {:.5f}".format(np.median(X)))
print("Confidence interval at 99%: {}".format(pci))
print("To be compared with: ({}, {})".format(np.median(X)-3*scale/np.sqrt(len(X)), np.median(X)+3*scale/np.sqrt(len(X))))

Median: 9.99912
Confidence interval at 99%: (9.990545100476202, 10.007734065899768)
To be compared with: (9.990119056062714, 10.008119056062714)